Gavin Hartnett

Gavin Hartnett

Theoretical Physicist and Machine Learning Researcher

Quantum Computing Research

Research

My quantum computing research focuses on developing practical algorithms and error mitigation techniques for near-term quantum devices. As a research scientist at Q-CTRL, I lead the Applications and Algorithms Team, which focuses on quantum applications and large-scale demonstrations while also supporting research into quantum control techniques that enhance Q-CTRL’s error suppression library. Our work addresses critical challenges in making quantum computing practical for current noisy intermediate-scale quantum (NISQ) devices, with applications spanning quantum optimization, quantum simulation, and quantum machine learning. These efforts bridge theoretical quantum advantage with real-world hardware implementations.

Circuit Ranker Pipeline

Recent Papers:

  • Resource-Efficient Context-Aware Dynamical Decoupling Embedding for Arbitrary Large-Scale Quantum Algorithms: Developed comprehensive frameworks for suppressing errors in quantum circuits without the full overhead of quantum error correction. This includes novel dynamical decoupling techniques that scale to arbitrary large circuits and achieve orders of magnitude improvement in circuit fidelities. Published in PRX Quantum (2025).

  • Quantum optimization using a 127-qubit gate-model IBM quantum computer can outperform quantum annealers for nontrivial binary optimization problems: Led development of quantum solvers for binary optimization problems that consistently outperform classical and quantum annealing approaches. Demonstrated successful optimization on 127-qubit systems with approximation ratios ≥99.5% for Max-Cut and higher-order spin-glass problems. This work represents the largest quantum optimizations successfully solved on hardware to date. Available via arXiv.

  • Achieving Computational Gains with Quantum Error-Correction Primitives: Demonstrated that strategic application of QEC primitives without full logical encoding can yield significant computational advantages on current quantum processors. Achieved record-setting 75-qubit GHZ state generation with genuine multipartite entanglement while maintaining reasonable overhead (12% qubit overhead, 78% shot discard rate). Published in PRX Quantum (2025).

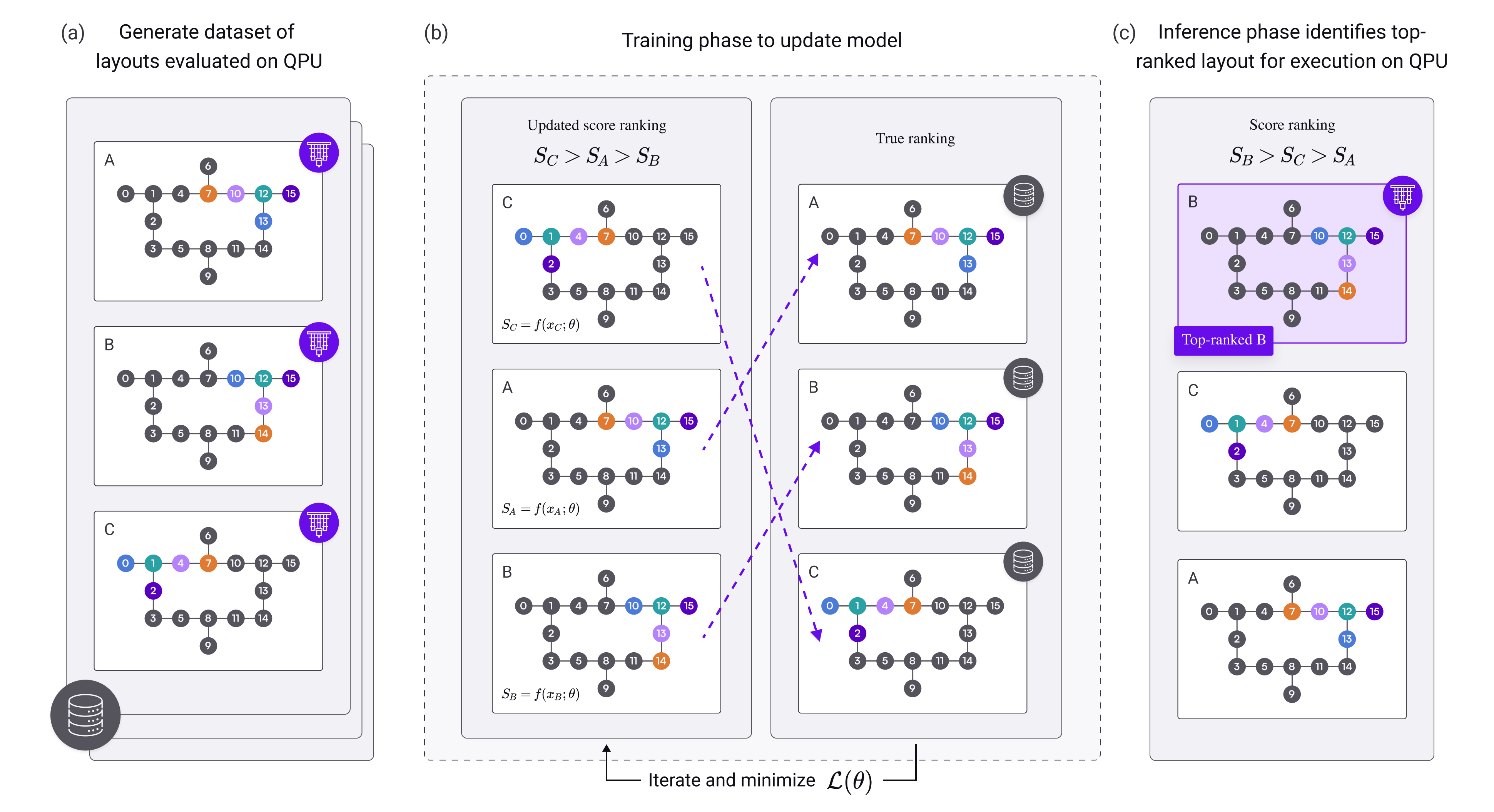
  • Learning to rank quantum circuits for hardware-optimized performance enhancement: Developed machine learning approaches for ranking quantum circuit layouts based on expected hardware performance. Created physics-based phenomenological models that reduce selection error by 3.2× compared to random selection and 1.8× compared to baseline methods. Published in Quantum (2024).

  • Twisty-puzzle-inspired approach to Clifford synthesis: Created novel algorithms for decomposing Clifford operations into hardware-native gates using machine learning techniques inspired by Rubik’s Cube solving algorithms (the Rubik’s Cube being the most famous example of a twisty puzzle). The approach often achieves better gate counts than existing methods while being flexible enough to incorporate arbitrary gate sets and device topologies. Published in Physical Review A (2024). Open-source implementation available on GitHub.